序贯均衡由 kreps 和 wilson 于 1982 年提出. 它要求参与人必须对她的每个信息集上的节点具有一个信念, 即使这个博弈不是贝叶斯博弈. 序贯均衡还要求参与人的信念是一致的.
序贯均衡包括一个策略组合 \(σ\) 和信念系统 \(μ\):
称 \((σ, μ)\) 是序贯均衡, 若:
给定信念系统 \(μ\), 策略组合 \(σ\) 是(序贯)理性的. 也就是说, 单方面偏离均衡策略对参与人 i 没有好处.
对于博弈结果中能到达的节点, 信念由贝叶斯法则决定.
由于贝叶斯法则对于那些博弈结果中无法到达的节点不起作用, 序贯均衡要求 \(μ\) 要额外满足一致性.
存在某个完全随机的策略组合序列 \(\{ σ^m \}\) 和由其决定的信念系统序列 \(\{ β^m \}\), 使得 \((σ , β)\) 是 \((σ^m , β^m)\) 在 \(m \to +\infty\) 时的极限.
和子博弈精炼均衡相比, 序贯均衡要求参与人在每个信息集都有一个信念. 对于简单的博弈, 信念通常不需要使用贝叶斯法则, 而是直接由对手的策略决定. 比如石头剪刀布博弈, 其序贯均衡为所有人都使用混合策略 (1/3, 1/3, 1/3), 同时信息集上的概率分布也是 (1/3, 1/3, 1/3).
序贯均衡定义中的前两个条件很容易理解. 事实上, 仅凭这两个条件 (再加上参与人总是有某个明确信念这个限制) 得到的解概念就已经强于子博弈精炼均衡. 但是, 序贯均衡的定义没有止步于此, 它还有一个看似奇怪的“一致性”条件.
定义中的第三个一致性要求的动机是明显的: 对于贝叶斯法则无法适用的情况, 我们如果想强行使用贝叶斯法则, 可以对策略组合 \(σ\) 进行微扰, 使其完全随机化. 这样可以得到某个序列 \(\{ σ^m \}\), 并通过贝叶斯法则推导出其对应的信念系统序列 \(\{ β^m \}\). 最后, 检验 \(β\) 是不是这个序列的极限即可.
但是, 这个一致性条件在实际应用中并不方便: 它没有明确说明如何对策略组合 \(σ\) 进行微扰. 由于 σ 是一个 N 维向量, 并且每个分量 \(σ_i\) 的复杂程度也取决于这个博弈的复杂程度, 肯定存在很多不同的将 \(σ\) 完全随机化的方法. 但是, 要验证 \((σ , β)\) 是序贯均衡, 我们只需找到一个满足条件的完全随机序列即可, 不需要保证 \((σ , β)\) 是所有可能的微扰序列的极限. 但据我所知, kreps 和 wilson 没有给出一个通行的找随机化序列的算法 😳
此外, kreps 和 wilson 在构造这个“一致性”条件时, 并没有要求序列 \((σ^m , β^m)\) 中的策略组合 \(σ^m\) 在给定 \(β^m\) 时是最优的. 对于博弈论老手, 这似乎不太自然: 为什么不先把张三的严格劣策略排掉, 再考虑张三的完全随机策略序列呢?
我个人的理解是: “一致性”条件仅仅是对信念的要求, 而不是对于策略 \(σ\) 的要求. 策略 \(σ\) 的合理性已经由定义中的条件一 (序贯理性) 保证了. 我们只需要找到某个可以收敛到 σ 的(完全随机)策略组合序列, 使得它由贝叶斯法则生成的信念系统序列可以收敛到 β 即可. 至于这些 (完全随机的) 策略组合是否涉及严格劣策略, 则无需过多关注.
我们用几个例子来测试序贯均衡的威力.
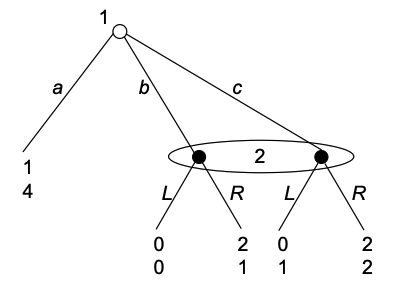
在这个例子中, 参与人 2 只要有一个明确的信念, 就一定会选择行动 R. 给定参与人 2 选 R, 行动 b 和 c 都是参与人 1 的最优反应. 进一步, 给定参与人 1 在行动 b 和 c 之间依照概率 \((p, 1-p)\) 进行随机, 参与人 2 的信念也是 \((p, 1-p)\).
在这个例子中, 关于信念系统的一致性要求没有起到任何实质性作用. 请读者自行验证, 对任意 \(p \in [0,1]\), 都可以找到参与人 1 的完全随机策略序列, 使得它对应的信念系统收敛到 \((p, 1-p)\).
考虑如下扩展型博弈: 自然先行动, 然后是参与人 1 和参与人 2. 自然以 (1/2,1/2) 的概率随机选择一个行动.
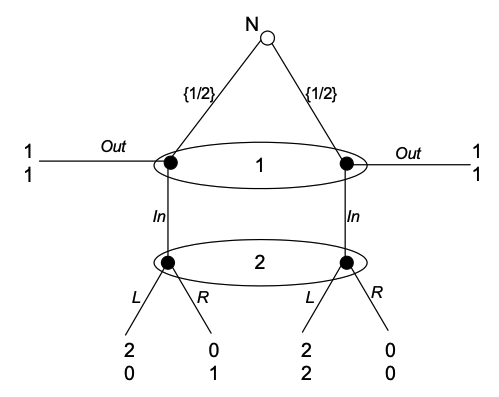
在这个博弈中, 参与人 2 唯一“合理”的信念是 (1/2,1/2), 因为她知道参与人 1 同样看不见自然的行动.
一致性要求形式化了这一直觉: 对参与人 1 的任意完全随机策略, 参与人 2 对应的贝叶斯信念都是 (1/2,1/2). 因此, 信念 (1/2,1/2) 是唯一满足一致性要求的信念.
这个信念下, 参与人 2 的最优行动是 L. 给定参与人 2 选 L, 参与人 1 的最优行动是 In.
在这个博弈中, 行为人 3 代替了例2中的自然. 见下图:
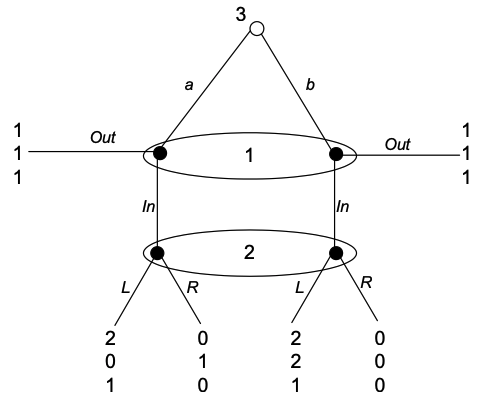
考虑如下策略组合: (Out, R, b). 不难验证, 它是纳什均衡. 同时, 为了让行动 R 构成参与人 2 的最优反应, 她的信念 \((p, 1-p)\) 必须满足 \(p \ge 2/3\). 也就是说, 参与人 2 必须相信, 当博弈进行到她的信息集时, 博弈路径经过左边节点的概率要大于经过右边节点的概率.
但是, 这样的信念似乎不太"合理". 原因如下:
一致性要求形式化了上述推理: 任何收敛到 (Out, R, b) 的策略组合序列, 其对应的信念系统的极限中, 参与人 2 的信念一定为 (0,1). 给定这个信念, 参与人 2 的最优行动是 L. 因此, (Out, R, b) 不是序贯均衡.
以上三个例子均来自 Debraj Ray 的讲义. Debraj 称例 3 中的推理体现了奥卡姆剃刀原则: 当参与人 2 发现博弈的进行偏离了原本的路径时, 应该默认这个偏离是一个最小偏离, 而不是一个大规模的偏离. 具体来说, 参与人 2 会认为只有参与人 1 单方面偏离了均衡, 而参与人 3 仍遵循她原本的策略行动.
细心的读者可能已经发现, 上述关于信念一致性的讨论基本只适用于参与人行动集有限的情形. 如果参与人行动集是一个连续的区间, 那么“通过微扰得到完全随机化策略序列”这个技巧就起不到任何作用 (请读者思考其中原因). Kreps 和 Wilson 的 1982 年论文中, 只讨论了参与人行动集有限的情形.
除了信念一致性外, 将序贯均衡这个概念推广到无穷博弈还有许多技术上的挑战. 目前, 这个问题的 state-of-art 应该是 Myerson 和 Reny (2020), 有兴趣的读者可以看看这篇文章: https://home.uchicago.edu/~rmyerson/research/seqm.pdf. 欢迎和我邮件讨论.
Kreps, David and Robert Wilson, (1982). "Sequential equilibria." Econometrica.
Debraj Ray (2006), Sequential Games with Incomplete Information. https://pages.nyu.edu/debraj/Courses/GameTheory2006/Notes/lect09.pdf
Myerson and Reny (2020), Perfect Conditional ε-Equilibria of Multi-Stage Games With Infinite Sets of Signals and Actions, Econometrica.