咬文嚼字: 不完备信息博弈 v.s. 贝叶斯博弈

本文从 Gibbons 博弈论教材中对精炼贝叶斯均衡这个概念的误用出发, 试图理清博弈论中 "贝叶斯" 这个概念的内涵. 我认为, 这种区分对于本科生学习博弈论是很有帮助的.

Gibbons 关于精炼贝叶斯均衡的误用

本科生博弈论教材中, 通常会将博弈按照 (i) 信息是否完备 和 (ii) 参与人是否同时行动分为四类, 并分别介绍四种解概念:

• 纳什均衡
• 子博弈精炼 (subgame-perfect) 纳什均衡
• 贝叶斯均衡
• 精炼贝叶斯均衡 (perfect bayesian equilibrium)

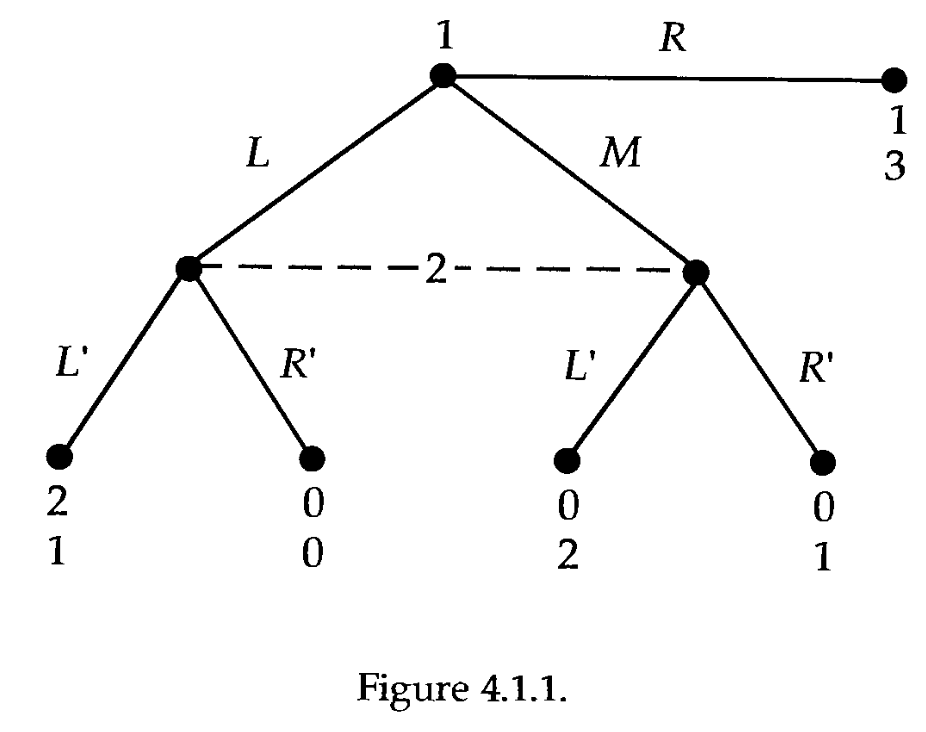
典型代表是 Gibbons 的 Game Theory for Applies Economists, 这本书在引入精炼贝叶斯均衡时用了如下例子 (英文版 P176, 图的编号为 Gibbons 原书编号):

上图的这个博弈有两个纳什均衡 \((R, R')\) 和 \((L, L')\). 其中第一个均衡不合理, 因为当参与人 1 未选 R 时, 参与人 2 的最优行动永远都只是 \(L'\). Gibbons 借这个例子引出精炼贝叶斯均衡这个解概念, 它要求参与人 2 始终对信息集有一个判断, 从而排除了 \((R, R')\) 这个结果.

许多博弈论入门书在介绍精炼贝叶斯均衡时, 都使用了和 Gibbons 类似的例子. 我认为这个例子不妥当, 因为这个博弈不是贝叶斯博弈, 贝叶斯均衡 (以及精炼贝叶斯均衡) 这类解概念不适用. 我们应该考虑纳什均衡相关的精炼 (子博弈精炼, 序贯均衡, 等等)

• 如果我自己的研究中涉及到这个博弈, 我会使用序贯均衡.

本科阶段的博弈论教学, 为了便于学生理解, 一些不重要的小错无关紧要. 但是, 我认为对这个博弈套用(精炼)贝叶斯均衡是一个比较严重的概念错误. 贝叶斯这个概念并不是博弈论特有的, 在机器学习、统计学等领域都很常用. 并且, 在所有这些学科中, "贝叶斯" 这个术语的基本涵义都是一致的. 对于有一定机器学习或统计学背景的学生, 接触 Gibbons 的这个例子会让他们对 "贝叶斯" 这个词的意思产生困惑, 进而觉得经济学家们对术语的使用十分随意.

统计学中的贝叶斯

以下说明出自维基百科 "贝叶斯统计" 相关词条:

贝叶斯统计的核心方法是基于贝叶斯公式，用取得的数据 (可记为 \(B\)) 对根据个人经验等先验信息对希望研究的命题或假设（可记为 \(A\)）先验概率 \(P(A)\) 进行修正，得到后验概率 \(P(A|B)\).

贝叶斯公式本身技术上十分简单, 任何概率论入门课程都会介绍贝叶斯公式. 贝叶斯方法的独特之处不在这个公式本身, 而在于假设参数满足某个先验分布. 历史上著名的“贝叶斯学派与频率学派”争论中, 主要的分歧点就在于先验分布这个设定是否合理.

博弈论中的贝叶斯

对于不完备信息博弈, 经济学家一般会引入参与人的类型空间和一个新的参与人 "自然", 并进一步假设参与人对其它参与人类型的分布存在某个"先验信念".¹ 这个过程就是大名鼎鼎的海萨尼转换. 当做出先验信念这个假定时, 博弈的参与人自然就成了贝叶斯的人, 这类博弈也被称为贝叶斯博弈. 贝叶斯博弈的解概念仍是纳什均衡, 但这个博弈的参与人比较特殊: 他们是相信贝叶斯学派的统计学家 (or, 理性人) 而不是相信频率学派的统计学家. 习惯上, 经济学家将这样的博弈称为贝叶斯博弈, 这类博弈的纳什均衡称为贝叶斯均衡 (或贝叶斯纳什均衡).

结语

让我们回到最开始 Gibbons 的例子. 这个博弈是完备信息博弈, 参与人也没有先验信念, 使用贝叶斯均衡这类均衡概念不妥当. 精炼贝叶斯均衡属于特殊的贝叶斯均衡.

我在本科时期, 对概率的相关哲学讨论很感兴趣, 这也是这篇文章的主要写作动机之一. 先验信念这个工具很酷, 因为它听起来很简单, 但在实践中又那么有用. 我试图在博弈论教学中让学生知道贝叶斯这个工具酷在哪, 而不是不加思索地套用精炼贝叶斯均衡这个复杂工具.

对精炼贝叶斯均衡和不完备信息博弈感兴趣的读者, 可以继续阅读以下内容. 后面的内容技术难度较高.

不完备信息博弈 v.s. 贝叶斯博弈

不完备信息博弈和贝叶斯博弈这两个概念不能划等号. 贝叶斯方法 (以及海萨尼转换) 是处理不完备信息博弈的常用方法, 但不是唯一方法.

最常见的非贝叶斯方法之一, 是只关注最坏情形的分析, 这时博弈的分析就不必引入先验信念. 最坏情形分析 (Worst-case analysis) 这个方法也常被计算机科学家用来分析算法效率. 关于这个方法在经济学的应用, 可以参考 Guo and Shmaya 近年的两篇文章: Regret-Minimizing Project Choice (2023) 和 Robust Monopoly Regulation (2023).

我并非相关方面的专家, 就此打住.

贝叶斯均衡和精炼贝叶斯均衡

Osborne 和 Rubinstein 关于贝叶斯博弈的定义如下 (英文版P25, Definition 25.1):

A Bayesian game consists of

• a finite set \(N\) (the set of players)
• a finite set \(\Omega\) (the set of states)

and for each player \(i \in N\)

• a set \(A_i\) (the set of actions available to player \(i\))
• a finite set \(T_i\) (the set of signals that may be observed by player \(i\)) and a function \(\tau_i : \Omega \to T_i\) (the signal function of player \(i\))
• a probability measure \(p_i\) on \(\Omega\) (the prior belief of player \(i\))
• a preference relation on the set of probability measures over \(A \times \Omega\) (the preference relation of player \(i\)), where \(A = \times_{j \in N} A_j\)

这个定义中明确要求了参与人是贝叶斯的 (i.e., 具有先验信念 \(p_i\)). 这里贝叶斯博弈是定义在状态空间上, 而非参与人的类型空间上, 后者可以看成是前者不失一般性的简约形式.

精炼贝叶斯均衡这个概念由 Fudenberg 和 Tirole 提出. 和序贯均衡这样适用于一般策略性博弈的均衡概念不同, 精炼贝叶斯均衡这个概念基于贝叶斯均衡, 并且只适用于一类特定的贝叶斯博弈. 由于精炼贝叶斯均衡这个解概念的描述比较复杂, 本文略去. 读者可以阅读 Osborne 和 Rubinstein P231 的 12.3 小节: "Games with Observable Actions: Perfect Bayesian Equilibrium."