目前为止, 我们讨论的学习算法都是在对如下条件概率建模: \[ p(y \mid x) \]
这种学习算法也被称为判别式学习算法 (Discriminant learning algorithm), 它的特点是直接利用 X 的信息来判别 y, 并且模型中不用描述 X 的分布.
我们接下来讨论另一种类型的学习算法: 生成式学习算法. 和判别式学习算法不同, 生成式学习算法中一般要规定数据 (X,Y) 的生成机制, 模型中需要描述 X 的分布信息.
我们主要在"分类"这个问题背景下讨论生成式学习算法.
考虑如下分类问题: 我们希望根据动物的某些特征来区分大象(\(y=1\))和狗(\(y=0\)).
不同于判别式算法, 生成式算法的基本步骤如下:
具体地, 我们用 \(y\) 表示一个样本是狗(0)还是大象(1), 那么条件概率 \(p(x \mid y=0)\) 描述了狗的特征分布, \(p(x \mid y=1)\) 描述了大象的特征分布.
由于我们的目标是预测 (即预测给定 x 下 y 的值), 我们不用关注上面方程的分母. 因为: \[ \begin{aligned} \arg \max _{y} p(y \mid x) & =\arg \max _{y} \frac{p(x \mid y) p(y)}{p(x)} \\ & =\arg \max _{y} p(x \mid y) p(y) \end{aligned} \]
我们介绍的第一个生成学习算法是高斯判别分析 (GDA).
高斯判别分析假设每个具体类别下的 x 服从多元正态分布:
我们先简要回顾一下多元正态分布的性质, 再讨论高斯判别分析.
记 \(x\) 为 \(n\) 维连续随机变量. 最常用, 同时也最简单的高维连续随机变量是多元正态分布, 也称多元高斯分布.
多元正态分布由均值向量 \(\mu \in \mathbb{R}^{n}\) 和协方差矩阵 \(\Sigma \in \mathbb{R}^{n \times n}\) 参数化, 其中\(\Sigma \geq 0\)是对称且半正定的.
若 \(x \sim N(\mu, \Sigma)\), 其密度函数为: \[ p(x ; \mu, \Sigma)=\frac{1}{(2 \pi)^{n / 2}|\Sigma|^{1 / 2}} \exp \left(-\frac{1}{2}(x-\mu)^{T} \Sigma^{-1}(x-\mu)\right) \]
向量值随机变量 \(Z\) 的协方差为 \(\operatorname{Cov}(Z)=\mathrm{E}[(Z-\mathrm{E}[Z])(Z-\mathrm{E}[Z])^{T}]\).
如果\(X \sim N(\mu, \Sigma)\), 那么: \(\operatorname{Cov}(X)=\Sigma\).
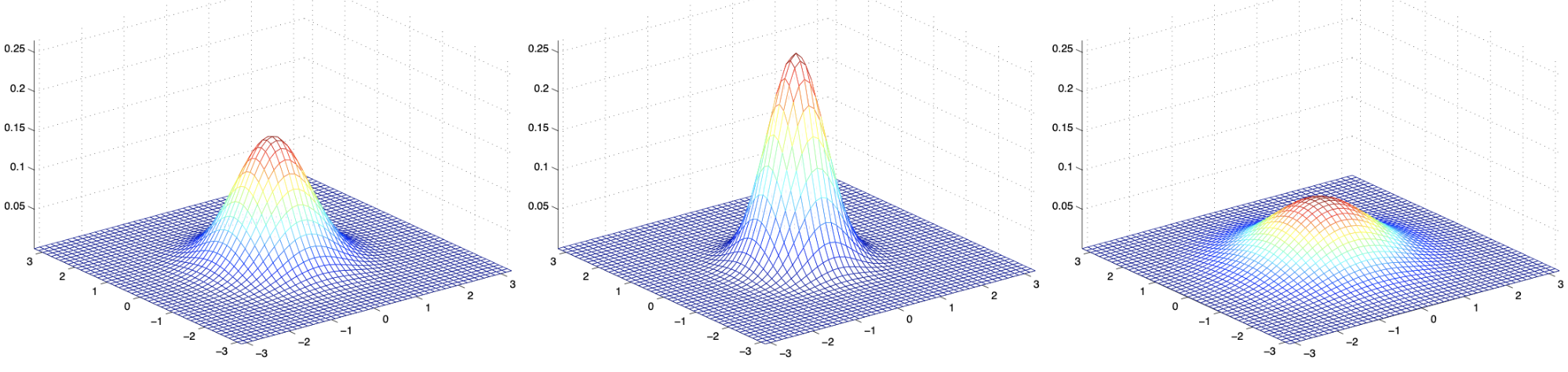
以下是(二维)高斯分布的一些示例. 它们的均值都是 (0,0), 区别在于协方差矩阵:

注: 借助 DeepSeek, 你可以很容易地在 R/Python 中绘制上面的 3D 概率密度图. 你应该动手试一试!
我们另外再看3个例子, 均值仍为零向量, 但协方差矩阵分别为: \[ \Sigma_1=\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right] \quad \Sigma_2=\left[\begin{array}{cc} 1 & 0.5 \\ 0.5 & 1 \end{array}\right] \quad \Sigma_3=\left[\begin{array}{cc} 1 & 0.8 \\ 0.8 & 1 \end{array}\right] \]
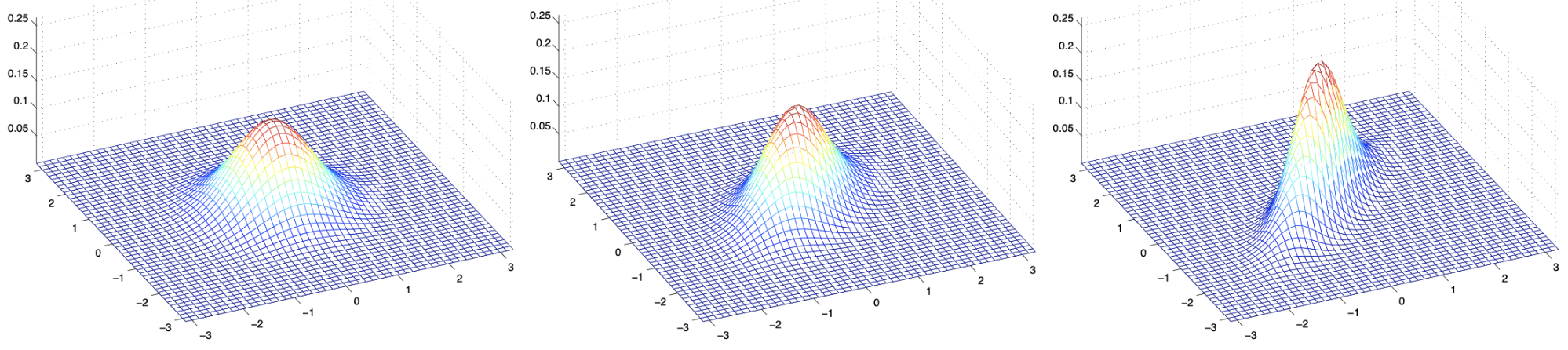
我们最后再看三个例子. 这回我们固定 \(\Sigma=I\), 只改变均值向量 \(\mu\).
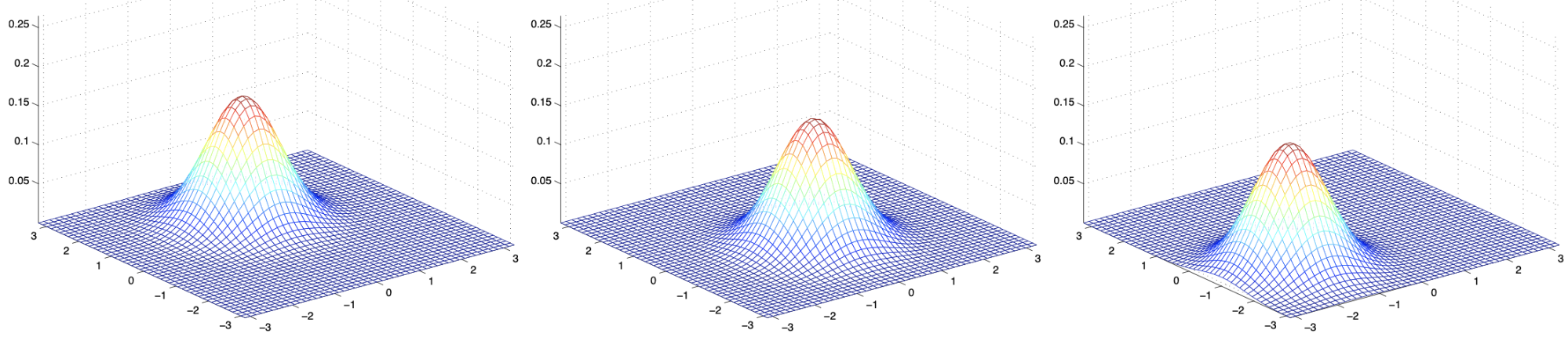
上图使用了\(\Sigma=I\),
均值分别为:
\[
\mu=\left[\begin{array}{l}
1 \\
0
\end{array}\right] ; \quad \mu=\left[\begin{array}{c}
-0.5 \\
0
\end{array}\right] ; \quad \mu=\left[\begin{array}{c}
-1 \\
-1.5
\end{array}\right]
\]
模型中的分布设定:
y, (x|y=0), 和 (x|y=1) 的密度函数如下:
\[ p(y) = \phi^y (1 - \phi)^{1-y} \]
\[ p(x \mid y = 0) = \frac{1}{(2\pi)^{n/2} |\Sigma|^{1/2}} \exp \left( -\frac{1}{2} (x - \mu_0)^T \Sigma^{-1} (x - \mu_0) \right) \]
\[ p(x \mid y = 1) = \frac{1}{(2\pi)^{n/2} |\Sigma|^{1/2}} \exp \left( -\frac{1}{2} (x - \mu_1)^T \Sigma^{-1} (x - \mu_1) \right) \]
模型参数: \(\phi\), \(\Sigma\), \(\mu_0\) and \(\mu_1\). 我们使用极大似然法来估计这些参数, 对数似然函数如下: \[ l(\phi, \mu_0, \mu_1, \Sigma) = \log \prod_{i=1}^{m} p(x^{(i)}, y^{(i)}; \phi, \mu_0, \mu_1, \Sigma) \]
\[ = \log \prod_{i=1}^{m} p(x^{(i)} \mid y^{(i)}; \mu_0, \mu_1, \Sigma) p(y^{(i)}; \phi) \]
由于正态分布和两点分布的"分析"性质很好, 我们可以直接得到参数的最大似然估计: \[ \begin{aligned} \phi & =\frac{1}{m} \sum_{i=1}^{m} 1\left\{y^{(i)}=1\right\} \\ \mu_{0} & =\frac{\sum_{i=1}^{m} 1\left\{y^{(i)}=0\right\} x^{(i)}}{\sum_{i=1}^{m} 1\left\{y^{(i)}=0\right\}} \\ \mu_{1} & =\frac{\sum_{i=1}^{m} 1\left\{y^{(i)}=1\right\} x^{(i)}}{\sum_{i=1}^{m} 1\left\{y^{(i)}=1\right\}} \\ \Sigma & =\frac{1}{m} \sum_{i=1}^{m}\left(x^{(i)}-\mu_{y^{(i)}}\right)\left(x^{(i)}-\mu_{y^{(i)}}\right)^{T} \end{aligned} \]
从图像上看, 高斯判别分析算法的操作如下:
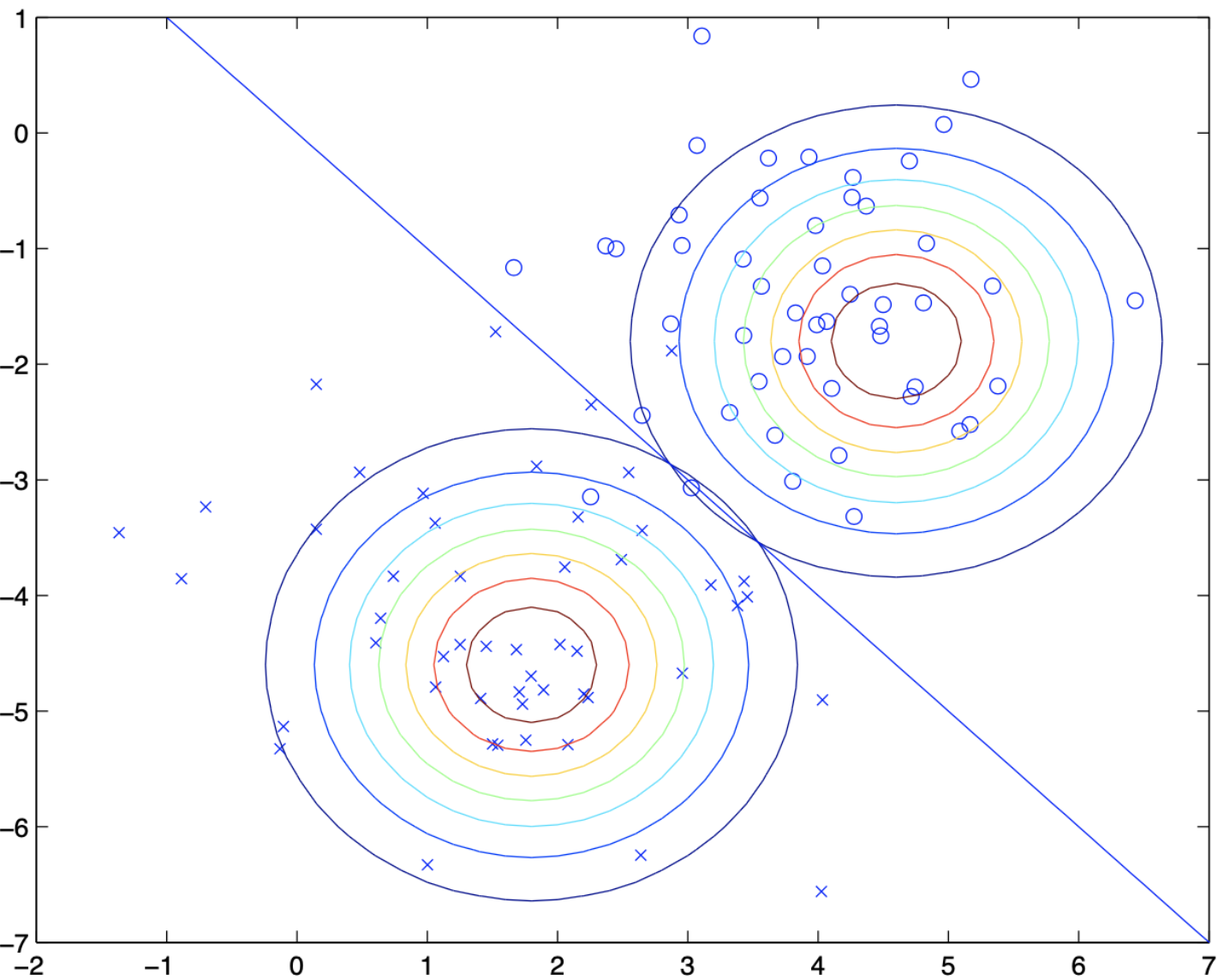
GDA 中, 如果我们将 \(p(y=1 | x; ϕ,μ_0,μ_1,Σ)\) 视为 x 的函数, 可以将它的表达式写成如下形式: \[ p\left(y=1 \mid x ; \phi, \Sigma, \mu_{0}, \mu_{1}\right)=\frac{1}{1+\exp \left(-θ^{T} x\right)} \]
虽然两者的判别规则的函数形式相同, 我们在用极大似然法训练模型时的算法不同. 因此, GDA和逻辑回归在相同数据集上训练时会给出不同的决策边界. 这时, 哪个模型更好呢?
总结: 由于逻辑回归比 GDA 更稳健, 在实践中逻辑回归比GDA更常用. 不过, 如果研究者事先知道数据集中的 \(X\) 近似服从多元高斯分布, 使用 GDA 的预测效果会更好.
一般来说, 判别模型的假设总是少于生成模型. 但是, 我们接下来讨论的朴素贝叶斯算法的性能非常好, 它在文本分类中(曾经)是最流行的算法.
在我们前面的讨论中, GDA 假设每个类别的 x 的多元正态分布具有相同的协方差矩阵. 在这个假设下, 我们得到的决策边界是线性的. 在有的文献中, 称这种类型的高斯判别分析为线性判别分析 (LDA).
和线性判别分析对应的概念是二次判别分析 (QDA):
QDA 分类器将观测值 \(x\) 分配到使得以下判别函数最大的类别, 其中 \(\phi_k\) 为类分布 \(p(y=k)\) 的估计: \[ \begin{aligned} \delta_{k}(x) & =-\frac{1}{2}\left(x-\mu_{k}\right)^{T} \boldsymbol{\Sigma}_{k}^{-1}\left(x-\mu_{k}\right)-\frac{1}{2} \log \left|\boldsymbol{\Sigma}_{k}\right|+\log \phi_{k} \\ & =-\frac{1}{2} x^{T} \boldsymbol{\Sigma}_{k}^{-1} x+x^{T} \boldsymbol{\Sigma}_{k}^{-1} \mu_{k}-\frac{1}{2} \mu_{k}^{T} \boldsymbol{\Sigma}_{k}^{-1} \mu_{k}-\frac{1}{2} \log \left|\boldsymbol{\Sigma}_{k}\right|+\log \phi_{k} \end{aligned} \]
与 LDA 不同, x在判别函数中以二次函数的形式出现, 这也是QDA得名的原因.
什么时候应该使用 LDA (即假设 K 个类别有着相同的协方差矩阵)?
答案在于偏差---方差权衡:
粗略地说, 如果训练集中的观测值相对较少 (此时降低方差至关重要), LDA 往往比 QDA 更可靠. 相反, 如果训练集很大 (此时分类器的方差就不是主要问题) 或协方差矩阵相同的假设明显不成立, 则应使用 QDA.