透明偏好下的空谈博弈

本文描述了两个沟通博弈 (communication game) 的小例子. 沟通博弈指的是这样一类两人序贯博弈: 送方 (Sender, S) 私下观察到真实状态, 并向收方 (Receiver, R) 发送信号; 随后收方行动. 空谈 (cheap talk) 博弈是沟通博弈的特殊情形. 空谈博弈中, 送方无信号成本.

透明偏好指送方的效用和状态无关. 比如, 张三 (行动方) 去商场买衣服, 商场导购员 (送方) 并不关心张三最后买的衣服是否合适, 只想最大化张三在商场的消费. 这个例子中, 状态表示商场服装和张三是否相称. 因此, 导购员的事后效用是状态无关的, 只取决于张三的行动.

例1: Lipnowski & Ravid (2020)

考虑如下两人空谈博弈. 政策制定者 (收方, R) 考虑是否要出台新政策 ( $a \in \{ a_1, a_2 \}$ ) 或维持现有政策不变 ( $a = a_0$ ). 每个决策 $a$ 带给 R 的效用取决于未知状态 $ω \in \{ ω_1, ω_2 \}$ , 具体如下:

	$a_0$	$a_1$	$a_2$
$ω_1$	0	1	$-3$
$ω_2$	0	$-3$	1

假设 R 关于状态的先验信念为 (1/2, 1/2). 这个信念下, R 的最优决策是 $a_0$ .

送方 (Sender, S) 私下观察到真实状态. 同时, S 的偏好很极端: 无论真实状态 $ω$ 是多少, S 都希望 R 会实施更激进的政策 (对应 $a_i$ 中下脚标 $i$ 更高): $\forall i \in\{ 0,1,2 \}$ , 当R选择 $a_i$ 时, S效用为 $i$ . 此时, S 的偏好是状态无关的.

不难验证, 如果 S 的信号发送策略是非随机的, 均衡一定是平凡的 (即均衡中 S 无法影响 R 的行动).

请读者思考, 如果考虑混合信号发送策略, S 能否通过空谈来影响 R 的决策?

例1解答

可以. 考虑如下 S 的信号发送策略:

$ω = ω_2$ 时, 发送 $m_2$
$ω = ω_1$ 时, 1/2概率发送 $m_1$ , 1/2概率发送 $m_2$

R 的后验信念和行动:

收到 $m_1$ 时, R 确定状态一定为 $ω_1$ , 选 $a_1$
收到 $m_2$ 时, R 后验信念为 (1/4, 3/4), 她对 $a_2$ 和 $a_0$ 无差异. 我们考虑如下 R 的混合策略: 1/2 概率 $a_2$ , 1/2 概率 $a_0$

可以验证, 给定 R 的策略, S 对于发送信号 $m_1$ 和 $m_2$ 是无差异的. 因此, 上述描述符合均衡定义, 其中 R 的均衡效用为 1/4.

承诺

如果 R 可以进行承诺 (commitment), 他可以进一步提高状态和行动相配的概率. 考虑如下 R 承诺:

如果收到 $m_1$ , 选 $a_1$ ;
如果收到 $m_2$ , 一半概率选 $a_0$ , 一半概率选 $a_2$ .

可以验证, 此时 S 实话实说构成均衡. R 的均衡效用提高到 3/4.

Hu & Lei (2025) 基于这个例子分析了否决授权制度.

例2: Chakraborty & Harbaugh (2010)

两位候选人正在竞选州长. 记候选人 1 和候选人 2 的真实能力分别为 $θ_1$ 和 $θ_2$ , 且它们独立服从 $[0,1]$ 上的均匀分布.

某报社 (S) 私下观察到真实状态 $θ = (θ_1, θ_2)$ , 并向民众发送信号 $m ∈ \{ m^+,m^- \}$ , 民众收到信号 $m^+$ ( $m^-$ ) 后的后验信念记为 $a^+$ ( $a^-$ ). 为了简化描述, 读者可以直接将民众的后验信念解读为民众的行动.

该报社具有公开的政治立场: 相较于候选人 2, 她更偏好候选人 1. 具体地, 她的效用函数为 $U = ρ_1 a_1 + ρ_2 a_2$ , 且满足 $ρ_1 > ρ_2 > 0$ .

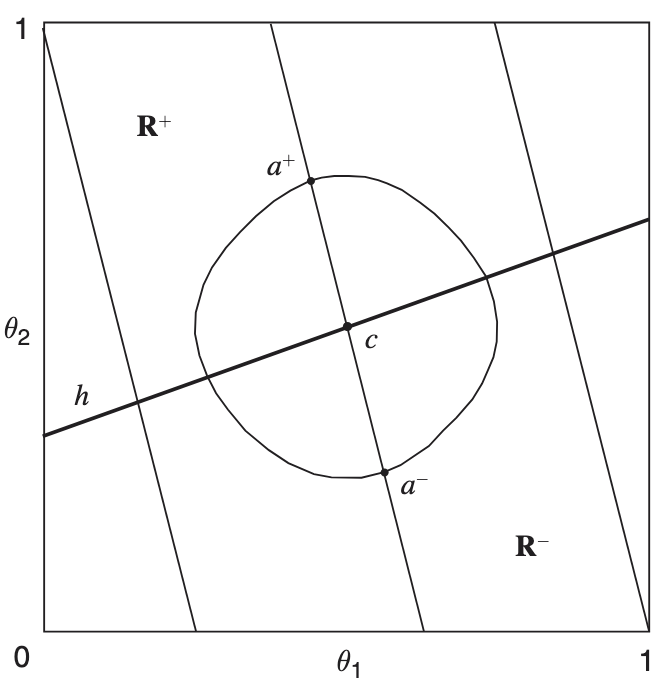
我们将状态空间表示为正方形; $c$ 点为正方形中心点, 它同时也是先验信念下民众的决策. 三条向右下倾斜的平行直线表示 S 的无差异曲线.

不同于例 1, 我们用状态空间的分划 (partition) 来描述 S 的信号发送策略. 我们只考虑直线分划, 每个直线分划会将状态空间分为两部分, 记直线上方(下方)的区域为 $R^+$ ( $R^-$ ). S 对应的策略如下:

当真实状态落在 $R^+$ ( $R^-$ ) 时, 发送 $m^+$ ( $m^-$ ).
对应的后验信念 $a^+$ 和 $a^-$ 分别为区域 $R^+$ 和 $R^-$ 的重心.

上图描述了如下非平凡均衡:

考虑一类特殊的直线分划: 这些直线都会通过点 c, 它们绕着 c 转一圈, 对应的后验信念构成图中的近似圆形.
考虑通过 c 的无差异曲线, 它和图中的近似圆形交于 $a^+$ 和 $a^-$ .
这对应如下均衡: 当二维状态落在 $R^+$ ( $R^-$ ) 区域时, 发送 $m^+$ ( $m^-$ ), 对应的后验信念为 $a^+$ ( $a^-$ ).
由于送方对于 $a^+$ 和 $a^-$ 无差异, 满足均衡条件.