熨平法: 卖盲盒和抽签配给

本文例子来自 Bulow and Roberts (1989), 可作为了解 Myerson 熨平法的敲门砖.

张三开了家小猪佩奇手办厂, 目标用户为 A 市幼儿园小朋友. 市场调研结果表明, A 市幼儿园一共有 20 万小猪佩奇手办的潜在消费者, 对应的需求函数如下: $$p(q) = 100-2q, \, q \in [0,20] \text{ ($q$ 单位为万)}$$

根据中级微观经济学的知识, 他为 A 市小朋友的决策建立了如下模型:

• 假设每个小朋友至多购买一个手办. 对小朋友 i, 手办给他的价值记为 $v_i$.

• 小朋友 i 的效用函数如下: $$u(a_i, v_i) = \begin{cases} v_i - p_i & \text{ if } a_i = 1 \\ 0 & \text{ if } a_i = 0 \end{cases}$$

  其中 $a_i = 1$ 表示小朋友 i 购买手办, 此时其效用为手办带给他的价值 $v_i$ 减去手办价格 $p_i$; $a_i = 0$ 表示小朋友 i 不购买手办, 此时效用为 0.

• 根据市场需求函数 $p(q)$ 的函数形式, 张三进一步做出如下合理假设: A 市每个小朋友 $i$ 对手办的估值 $v_i$ 服从区间 $[60,100]$ 上的均匀分布, 并且 $v_i$ 之间彼此独立.

• 小猪佩奇手办的边际成本为 0. 张三计算后发现, 手办的最优定价为 $p=60$, 此时销量为 $q=20$ 万, 恰好覆盖 A 市所有小朋友.

请读者验证: 张三关于 $v_i$ 分布的假设和需求函数 $p(q)$ 是一致的, 且需求 $p(q)$ 下的最优定价恰好覆盖整个市场.

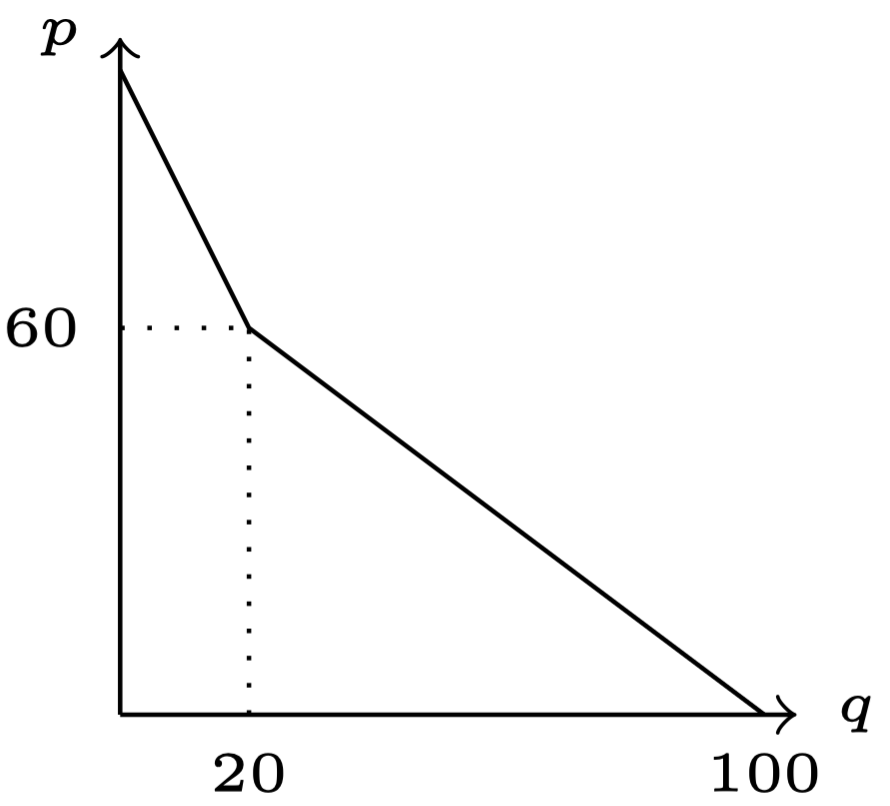
张三下令工厂生产 20 万件手办. 半年后, 工厂生产完毕, 张三准备以 60元/件的价格在 A 市发售. 但在此时, 助手李四报告说, 销售团队又联系到了 B 市的幼儿园. B 市虽然不及 A 市富裕, 但小朋友人数远超 A 市. 市场调研结果表明, B 市有 80 万小朋友对小猪佩奇手办感兴趣. 因此, A 市和 B 市总计有 20+80=100 万潜在消费者, 总的市场需求如下: $$p(q) = \begin{cases} 100-2q, &\text{if } q \in [0,20] \\ 70 - q/2, &\text{if } q \in [20,100] \end{cases}$$

$p(q)$ 函数图像如下, 注意在 $q=20$ 处的拐点:

由于产品上市在即, 公司已来不及生产更多手办, 如何将已生产的 20 万手办用更高价卖出? 张三和李四展开了激烈讨论:

👦🏻 李四:

如果在 A 市和 B 市同时进行销售, 并制定不同价格, 能否提高总销售收入?

👧🏻 张三:

此法似乎无用. 我们分析现在的总需求函数可知, B 市小朋友对手办的估值可以看成 $[20,60]$ 上的均匀分布, 而 A 市小朋友最低估值也有 $60$. 由于我们只有20万存货, 只够卖给经济更富裕的 A 市小朋友.

👦🏻 李四:

确实如此. 看来新增的 B 市小朋友客户对提高公司收入无用. 站在公司立场上看, 他们都是低价值客户. 这样的话, 我们还是维持原定销售计划不变?

张三没有马上附和李四. 他留意到了需求函数 $p(q)$ 的拐点, 这是他没有处理过的类型. 他决定邮件请教经济学教授 👩🏻‍🏫 王五. 很快, 张三就收到了王五的回复. 专家毕竟是专家, 王五教授竟真的找到了一种提高公司收入的方法.

王五教授 👩🏻‍🏫 的回信

张三你好:

感谢来信. 你的初步分析中, 根据需求曲线反推小朋友客户的行为决策的思路很好. 虽然 B 市由于经济欠发达, 消费者的支付意愿低于 A 市, 但 B 市小朋友对提高你的销售收入也是有帮助的. 限于时间, 我将直接告知你此时的最优销售策略. 如果你想明白其中原理, 可以用 Myerson ironing 作为关键字进行检索, 或者来学校旁听我的《机制设计》课程.

在原本的销售计划中, 手办定价为 60, 公司总收入为 20×60=1200万. 新的销售计划中, 你应该同时销售两种产品:

(a) 小猪佩奇手办, 定价为 65, 准备15万件.

(b) 小猪佩奇手办盲盒, 定价为 55/3, 准备15万件, 每个盲盒只有 1/3 的概率可以开出小猪佩奇.

新的方案下, 你的收入为 65×15+55/3×15=1250万>1200万. 可以验证:

• 估值为 $v \in [70,100]$ 的 A 市消费者会选择购买手办, 这批用户人数为 (100-70)/2=15万. 他们的行为是激励相容的, 因为 $$v - 65 \ge v/3 - 55/3$$
• 估值为 $v \in [55,70]$ A 市和 B 市消费者会选择购买盲盒, 这批用户人数为 (70-55)×2-15=15万. 他们的行为也是激励相容的: $$v/3 -55/3 \ge v - 65$$

除了卖盲盒外, 你也可以使用抽签配给法来实现1250万的收入. 具体如下:

• 每位小朋友可以从以下两个方案选一个:

  (a) 花费 65 元直接购买手办

  (b) 花费 55 元参与手办抽奖, 中奖率为 1/3, 奖品为小猪佩奇手办. 对于没有抽中的小朋友, 55 元将全部退回.

• 请自行验证, 抽签配给法的收入也是 1250 万元.

祝好,
王五 👩🏻‍🏫