前文介绍了贝叶斯相关均衡(BCE)的定义以及 BCE 的三种不同解读:
(1) 布莱克威尔比较定理在多人决策情形下的拓展;
(2) 当研究者不了解参与人的额外信息结构时, 可将所有 BCE 的集合视为博弈结果的稳健预测;
(3) 信息设计的理解视角: 信息设计者通过提供额外信息结构, 所能实现的贝叶斯均衡结果 = 原博弈的 BCE, 原博弈的 BCE 可以用概率约束+遵从约束刻画.
本文介绍三个BCE的例子。第一个例子涉及稳健预测的视角,后两个例子则是基于信息设计的视角。
这个例子来自 B&M (2013). 考虑如下单人决策问题:
状态:
先验信念: 均匀分布
行动:
效用: 如果行动 和状态 下角标一致, 效用为 1; 否则为 0.
考虑如下对称信息结构:
, .
令 表示决策规则. 其中, 表示状态和类型为 时, 协调者建议选择行动 的概率.
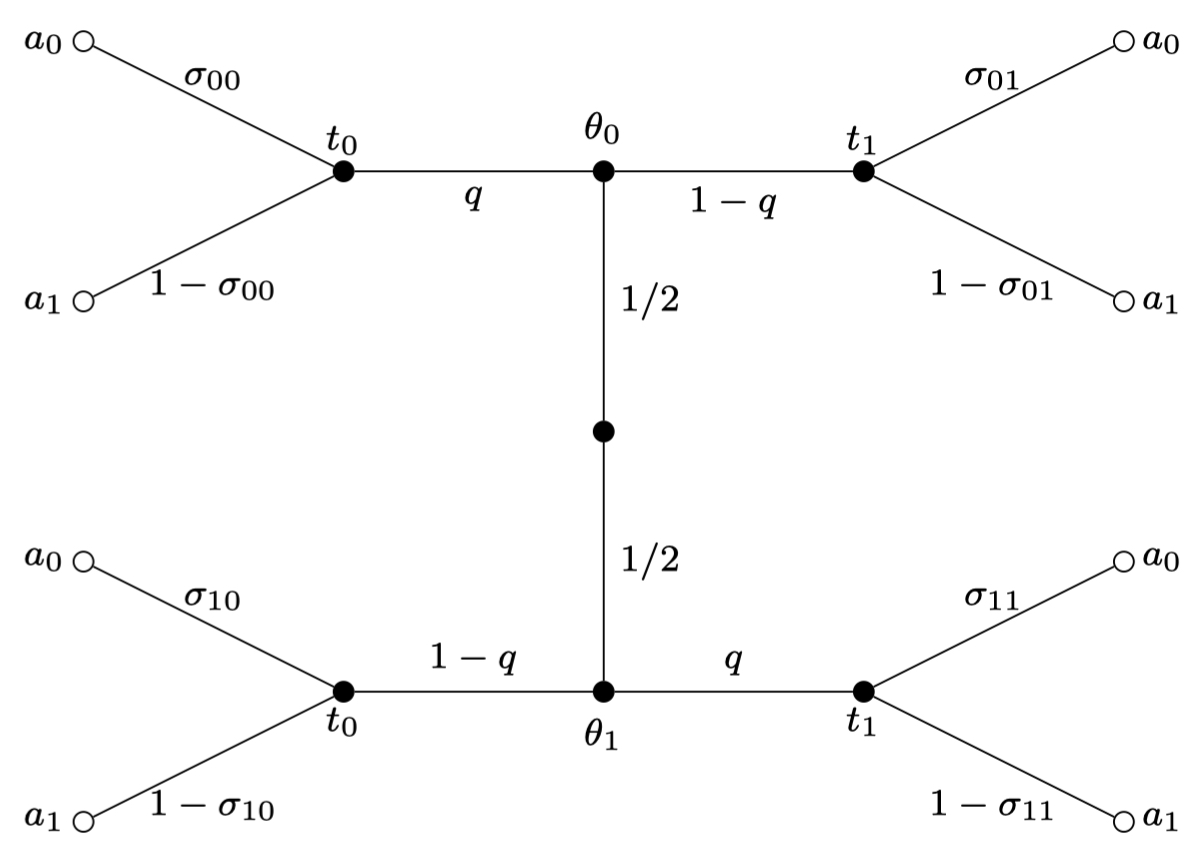
上述不确定过程对应的分叉路径如下, 其中每个路径上的标记为对应概率:
\usetikzlibrary{patterns,calc}
\begin{tikzpicture}[scale=1.3,font=\footnotesize]
\tikzstyle{solid node}=[circle,draw,inner sep=1.5,fill=black]
\tikzstyle{hollow node}=[circle,draw,inner sep=1.5]
\tikzstyle{level 1}=[level distance=15mm, sibling distance=1cm]
\tikzstyle{level 2}=[level distance=15mm, sibling distance=1.5cm]
\tikzstyle{level 3}=[level distance=15mm, sibling distance=1.5cm]
\node(0)[solid node,label=above:{}]{}
child[grow=down]{node[solid node, label=below:{${θ}_1$}]{}
child[grow = left]{node(1)[solid node, label=below right:{ }]{}
child{node[hollow node, label=left:{ }]{}
edge from parent node[above]{${\sigma}_{10}$}
}
child{node[hollow node, label=left:{ }]{}
edge from parent node[below, yshift=-0.13cm]{$1 - {\sigma}_{10}$}
}
edge from parent node[above]{$1-q$}
}
child[grow = right]{node(2)[solid node, label=below left:{ }]{}
child{node[hollow node, label=right:{ }]{}
edge from parent node[below, yshift=-0.13cm]{$1 - {\sigma}_{11}$}
}
child{node[hollow node, label=right:{ }]{}
edge from parent node[above]{${\sigma}_{11}$}
}
edge from parent node[above]{$q$}
}
edge from parent node[right, xshift=4, align=center]{ }
}
%% up branches
child[grow=up]{node[solid node, label=above:{${θ}_0$}]{}
child[grow = left]{node(3)[solid node, label=above right :{ }]{}
child{node[hollow node, label=left:{ }]{}
edge from parent node[above]{${\sigma}_{00}$}
}
child{node[hollow node, label=left:{ }]{}
edge from parent node[below, yshift=-0.13cm]{$1 - {\sigma}_{00}$}
}
edge from parent node[below]{$q$}
}
child[grow = right]{node(4)[solid node, label=above left :{ }]{}
child{node[hollow node, label=right:{ }]{}
edge from parent node[below, yshift=-0.13cm]{$1 - {\sigma}_{01}$}
}
child{node[hollow node, label=right:{ }]{}
edge from parent node[above]{${\sigma}_{01}$}
}
edge from parent node[below]{$1-q$}
}
edge from parent node[right, xshift=4, align=center]{ }
};
\node at (0,0.751) [right] {$1/2$};
\node at (0,-0.751) [right] {$1/2$};
\node at (1.50, 1.50) [above] {$t_1$};
\node at (-1.50, 1.50) [above] {$t_0$};
\node at (1.50, -1.50) [below] {$t_1$};
\node at (-1.50, -1.50) [below] {$t_0$};
\node at (3.01 , 2.24) [right] {$a_0$};
\node at (3.01 , 0.74) [right] {$a_1$};
\node at (3.01 , -2.24) [right] {$a_1$};
\node at (3.01 , -0.74) [right] {$a_0$};
\node at (-3.01 , 2.24) [left] {$a_0$};
\node at (-3.01 , 0.74) [left] {$a_1$};
\node at (-3.01 , -2.24) [left] {$a_1$};
\node at (-3.01 , -0.74) [left] {$a_0$};
\end{tikzpicture}
若 构成BCE, 其对应的四个不等式约束 (即遵从约束) 如下:
这四个遵从约束, 加上四个概率约束 , 刻画了所有的贝叶斯相关均衡 .
令 表示博弈结果, 其中 表示状态 时选择行动 的概率. 显然, 最理想的博弈结果是 , 此时决策者的效用为 1.
是均衡结果, 当且仅当存在满足四个遵从约束+四个概率约束的 使得
接下来我们将关于 的八个约束翻译为关于 的约束.
遵从约束 和 相加后得到 .
遵从约束 和 相加后得到 .
遵从约束 和 相加后得到 .
上面这三个不等式, 最强的是 . B&M (2013) 宣称, 这个不等式刻画了所有均衡结果.
本文作者注: 我没有验证这个结论的正确性, 它看起来似乎是对的.
下图表示了不同信号准确度 下的所有均衡结果, 即满足 的 . 粗黑点表示准确度 下对应的贝叶斯均衡结果.
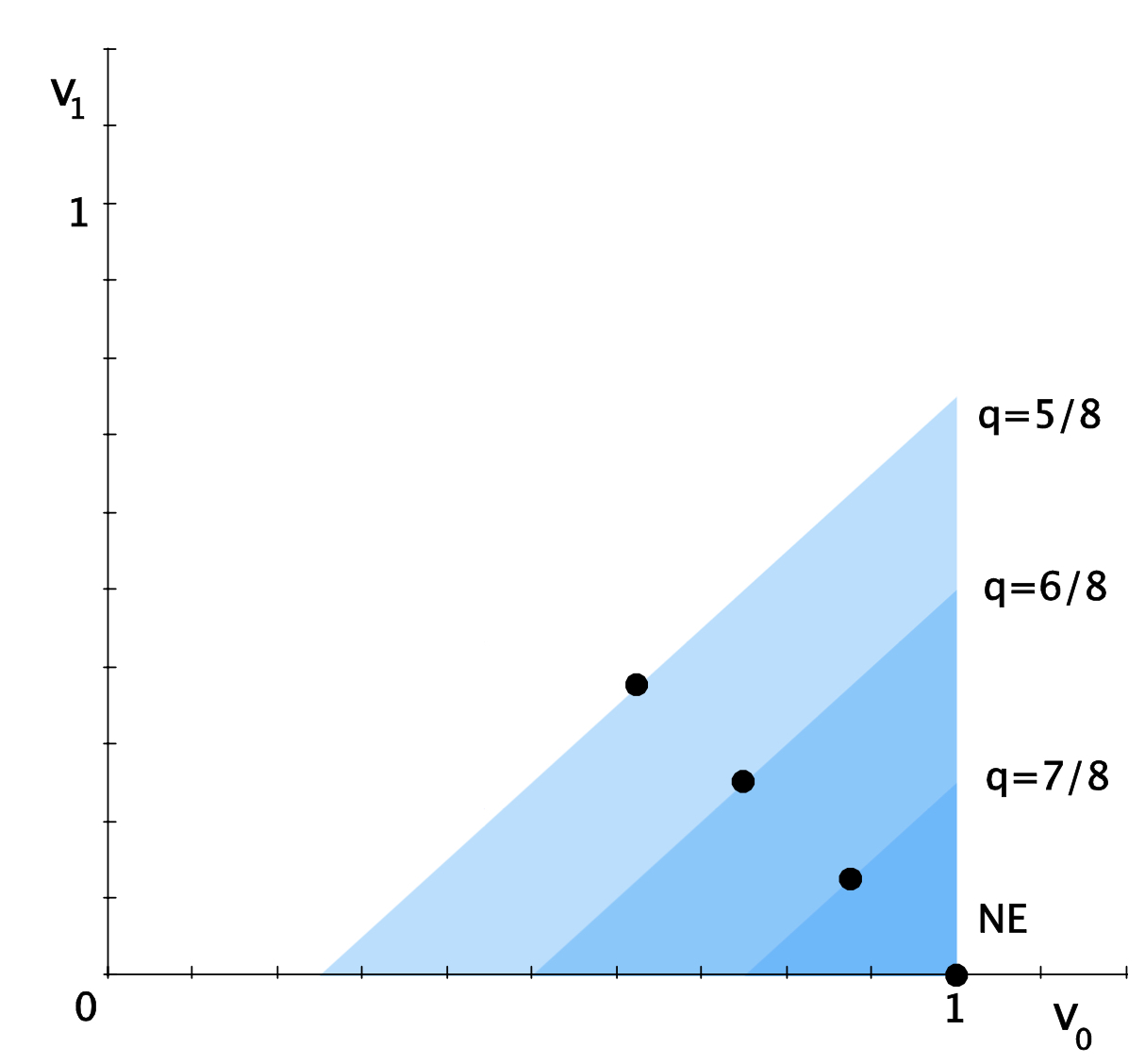
可以看出, 随着 不断变大, 得到的三角形 (ie, 均衡结果集) 严格变小. 当 时, 均衡结果集坍缩为 .
将这个例子和布莱克威尔的单人决策模型进行对比. 最开始准确度为 的公开信息结构可以视为第一个布莱克威尔实验, 随后协调者的行动建议是第二个布莱克威尔实验.
只有第一个实验时, 均衡结果为贝叶斯均衡, 即图中的黑点. 直觉上, 加入第二个实验后, 决策者效用只可能变多(或不变), 不可能变小. 图 2 中的三角形包括了所有决策者效用不严格上升的情形.
最后, 从稳健预测的角度来看: 若研究者仅知晓第一个公开信息结构, 但无法排除决策者拥有其它未知信息结构的可能性. 那么, 为给出博弈结果的稳健预测, 研究者给出的预测集是很宽泛的. 该预测集对应整个蓝色三角形区域.
上面的例 1 稍加修改后, 就可以变成 K&G (2011) 中的法官–检察官例子: 和 分别代表无罪和有罪, 和 表示法官的判决 (这里的决策者是法官).
K&G (2011) 例子的不同之处在于: 第一个公开信息结构 S 是平凡的, 并且法官的先验信念不是均匀分布. 不过, 基本分析方式是完全相同的. 我们可以先刻画出所有 BCE 对应的三角形, 这个三角形就是检察官通过信息设计所能诱导的所有博弈结果. 在确定了检察官的偏好之后, 检察官从所有可能的 BCE 中选择他最偏好的结果即可.
令 表示法官认为嫌疑犯无罪 () 的先验概率. 遵从约束为: 上面两个不等式约束加上两个概率约束 即可得到所有 BCE 构成的三角形.
K&G (2011) 的例子中, 检察官只有在法官选择 时才获得正效用 . 因此, 其效用为 , 它在 – 平面上的无差异曲线为一族平行线. 给定某个具体的先验信念 后, 可以画出 BCE 三角形和检察官的无差异曲线. 当 时, 检察官最偏好 BCE 三角形的左下顶点, 这个点就是贝叶斯劝说博弈中的均衡结果.
这个例子来自 Taneva (2019). 考虑如下极具对称性的 博弈:
两个参与人: 和
每个参与人有两个可能行动
两个可能状态 .
先验信念下, 两个状态是等可能的.
参与人不同状态下的效用如下表所示:
每个状态 对应的 (完备信息) 博弈均为协调博弈: 参与人都想选择行动 , 并且 是严格占优策略.
原(不完备信息)博弈存在三个对称贝叶斯均衡:
每个参与人都选
每个参与人都选
每个参与人按均等概率选择 和
引入第三个参与人: 信息设计者. 设计者总希望两位参与人行动不一致: 若 , 设计者效用为 ; 否则, 设计者效用为 .
如果信息设计者不提供额外信息, 即使均衡结果为设计者最优的贝叶斯均衡 (每个参与人按均等概率选择 和 ), 其效用也只有 1/2.
Seems ok
Too good to be true!
信息设计者可以通过控制信息披露, 来实现他所希望的 BCE 结果. 考虑如下对称的决策规则 , 它仅包含 两个参数:
任意给定状态下, 参数 表示两个参与人行动同时和状态一致的概率
任意给定状态下, 参与人 i (或 j) 行动和状态一致的概率为 .
接下来刻画所有对称贝叶斯相关均衡 , 只需描述参数 的可能取值即可. BCE 集合由遵从约束和概率约束确定, 其对应的 如下图所示.
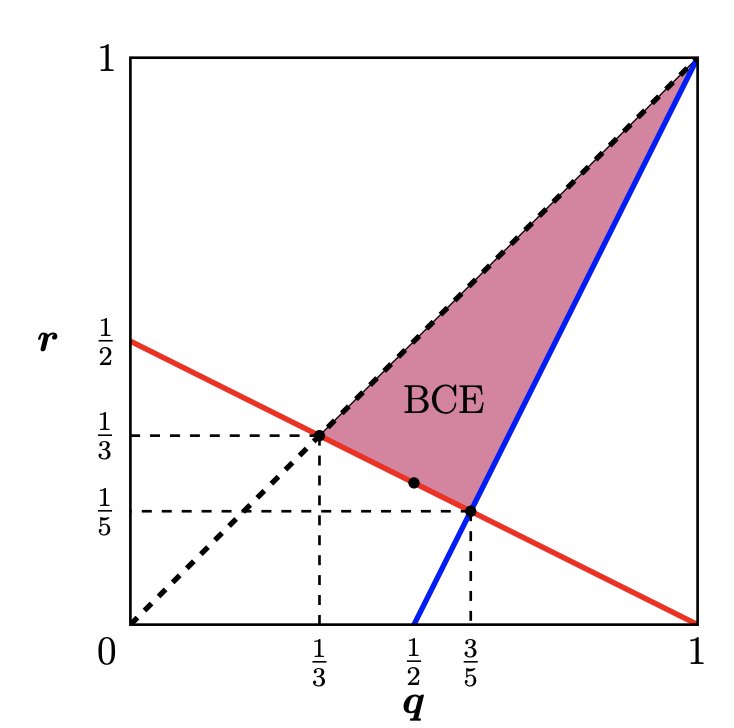
红线表示遵从约束, 它穿过点 (1/2,1/4), 即没有任何额外信息的混合贝叶斯均衡情形.
设计者最喜欢的结果是 或 . 但是, 这两个结果不是 BCE. BCE 集合可以看成是信息设计者的 “选择集”, 他可以通过信息设计来选择其最偏好的 BCE 结果.
下图平行的斜线表示设计者的无差异曲线, 设计者的最优 BCE 为三角形右下顶点: (3/5,1/5). 此时, 每个状态下两个参与人行动不一致的概率均为 4/5. 因此, 设计者的效用为 4/5.
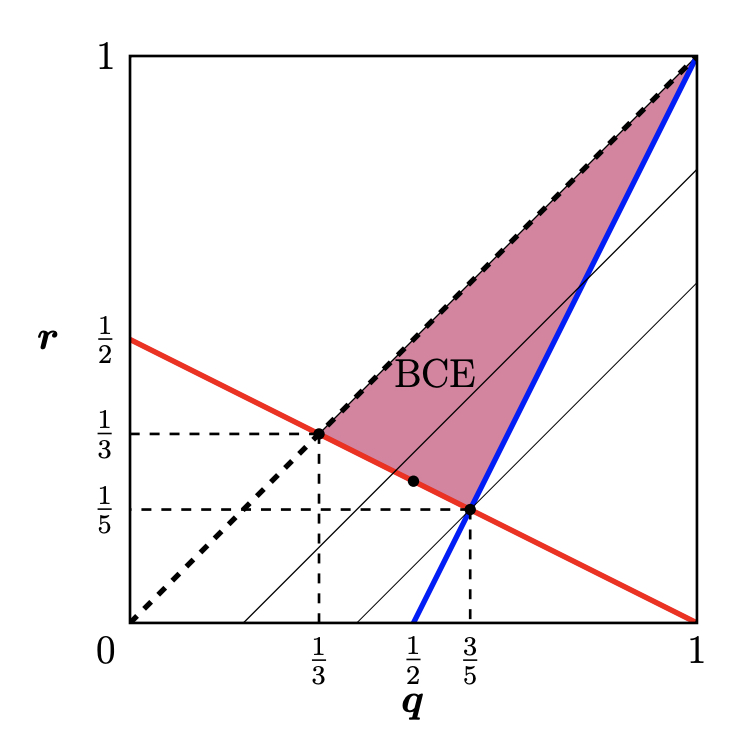
确定了设计者最优贝叶斯相关均衡 后, 可以进一步反推出最优信息结构. 在这个二元对称例子中, 最优信息结构 .
一些较复杂的 bce “例子”:
“Robust predictions in games with incomplete information,” (Bergemann&Morris, 2013). 这篇论文只算了”一个”例子: 存在连续多个参与人, 每个参与人收到一个私人高斯信号, 且参与人效用函数为二次式的不完备信息博弈.
“Robust Predictions in Coasian Bargaining,” (liu, 2022). 这篇文章讨论了科斯议价博弈中的 bce.
从论文标题可以看出, 这两篇文章都是从 “稳健预测” 的视角来使用bce 的. 如果你对 bce 的具体应用或计算感兴趣, 欢迎和我讨论.
我们分别对策略互补情形 (c>d),策略替代情形 (c<d),和 c=d>0 三种情况进行说明。每种情况下,BCE 对应的参数集合都是一个 q–r 平面上的凸多边形(三角形或四边形),我们只需说明顶点即可。
若 (策略互补情形), 所有 BCE 对应的参数 构成三角形, 其顶点为 , , (1,1)
若 , 所有 BCE 对应的参数 构成三角形, 其顶点为 (1/2,1/2), (1/2,0), (1,1).
若 (策略替代情形), 所有 BCE 对应的参数 构成凸四边形, 其顶点为 , , (1,1), (1/2,0).
要求解出上述三角形/四边形,只需写出对应的概率约束和遵从约束, 再加上一些代数小技巧即可。